- 10 January 2005 -

The Color of Money
by Danny Pascale, mailto:%20dpascale@BabelColor.com

Just a line in many contracts, the seemingly simple specification of "color" is the nightmare of many. From the unsatisfied but yielding customer to the redo-everything court order, using the wrong color always has an impact on your profit, either immediately, or with a more long-term effect due to the bad publicity you will get.

The problem is compounded by the fact that, even when you take great care in making sure that you meet the requirements, there is often a visible difference between the final result and what your customer (or you) wanted. A better understanding of the various languages of color—yes, you have to be fluent in many languages—can minimize these difficulties.

This article presents a short overview of the characterization of color and some of its languages. Part II will describe how you can translate between the various languages, some of the pitfalls to be aware of, and how you can judge the difference between two colors.

Like all scientific characterization methods, the description of color is built on many standards. For color, these standards have evolved slowly over the years, or should we say almost a century, with the uncommon trait that many old standards are still used, often more than recent ones, and that they all somewhat coexist peacefully.

This is due to the newer standards being devised on mathematical adaptations and transformations of fundamental measurements performed in the early 20th century. These fundamental measurements brought us the "standard observer,"in 1931, as defined by the CIE (Commission Internationale de l'Éclairage).

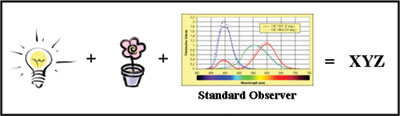
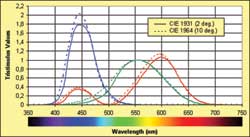Figure 1: The tristimulus values of the CIE 1931 (2 degrees) and CIE 1964 (10 degrees) standard observers. These are experimentally and mathematically derived representations of what the human eye perceives as red, green, and blue, and are the basis of all numerical color data.

The standard observer characterizes the human visual system as sensitive in three broad and overlapping bands of color. One of the bands is mainly over the red region of the spectrum, even if it extends in the blue region, and the others cover the green and blue regions (see Figure 1). The values in all three bands for a given wavelength are called tristimulus values.

The colors we can see extend from about 380 nm, a deep blue color, up to 720 nm in the red region. Ultraviolet, which is nonvisible although it is readily absorbed by the skin, can be found below the 380- nm limit; going down even further in wavelengths would bring us to X-rays. On the long wavelengths side, we find the near-infrared, just above the 720-nm limit, followed by the mid-infrared around 10,000 nm, a zone used by devices called "thermal imagers," which can "see" the heat emitted by objects or persons.

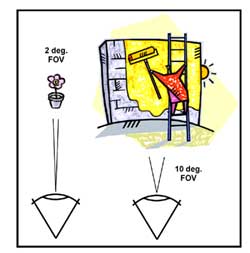Figure 2: The geometry of the 2 degrees and 10 degrees standard observers. The eye has more color sensors in the narrower field of view (FOV) and our perception of color is not the same as for the larger FOV. Our color perception decreases steadily for FOVs larger than 10 degrees.

The tristimulus values are not the wavelength response of the eye, although they can be associated to such a characterization, but a mathematical representation of how the eye and brain process colors of different wavelengths; it is the basis of how colors are measured. The CIE standard observer was defined using color patches subtending a 2 degrees field of view (FOV) with the eye (see Figure 2), where the eye has its highest density of color sensors (cones). This geometry corresponds well to color patches seen in images where many colors are seen next to one another. The computer-graphics world is almost entirely based on the 2 degrees observer.

In 1964, another standard observer was devised for color patches subtending 10 degrees FOVs with the eye; the CIE 1964 10 degrees observer. This larger FOV encompasses almost all the eye’s color sensors (i.e. the human eye is much less sensitive to color off-axis). It also more closely corresponds to the perception of large, uniformly colored expanses such as walls. Although at first sight it might seem that the CIE 1964 observer is better suited for painted surfaces characterization, this is not the case since the two observers describe a measuring method and, as long as you present results in association with the method, they both remain perfectly accurate. For instance, if you have a reference card and a large wall where both are measured as having the same color coordinates using the 2 degrees geometry, the wall and card will most likely look the same when subtending a 10 degrees FOV.

A color without light is black. A color with light is never the same color. The perception of a color is influenced by the spectral content of the light source, the viewing environment, the surface finish, and your brain’s memory. If you compare a white sheet of paper held in front of a window at midday when there is a bright sun, with a similar sheet held nearby so that you can simultaneously see both, under a 60 W light bulb, the one under the light bulb will look much yellower. The brain part comes into effect when you look at these sheets separately at different moments; in this case you will vow that they are of the same white. More on that subject later.

* Correlated temperature

In comparison, colors will be perceived differently under various lights, thus the importance of defining the light source, the illuminant, in colorimetry terms. Many standard illuminants have been defined over the years. They are called by short descriptions such as C (CIE illuminant C), which stands for "North Sky Daylight, 6,774 Kelvin;" or D50, which stands for "Daylight 5,000 Kelvin," the latter one often used for color rendering. The Kelvin is a temperature unit where zero Kelvin is the absolute zero (equal to -273 degrees Celsius) and where one Kelvin step is the same as a one degree Celsius step. A 5,000 Kelvin illuminant has a spectrum that corresponds to the light emitted by a black body (look at it as a calibrated piece of steel) heated to this temperature. As with the stars in the sky or forged metal, the hotter the temperature, the bluer it becomes. Illuminant D65, a very common illuminant for computer screens, corresponds to a 6,500 Kelvin temperature and is visibly bluer than D50. Common standard illuminants are given in Table I.

We now have the two basic elements of color characterization: a standard observer and an illuminant. These two combine to give us color coordinates. Here is the basic setup for color patches (measured by reflection). A calibrated light is shone on a color sample. The measurement setup is usually configured in a geometry that minimizes the amount of light due to surface reflections. In one of the standard geometries, the illuminant is positioned at 90 degrees (perpendicular) over the sample, and the detector is positioned at 45 degrees relatively to the sample surface; switching the illuminant and detector is an equivalent setup.

This way, the "tru" color of the surface is measured, without the portion of the illuminant that could be reflected by a polished surface acting as a mirror. In real life, however, you do have more or less of this effect and you may want to quantify it. This is discussed in the next section.

Figure 3: XYZ color coordinates are obtained by illuminating a color sample with a characterized illuminant and processing the reflected spectra with the standard observer functions. XYZ is considered "raw” data, the one from which other notations are derived.

The diffused light falling on the detector is analyzed in terms of what quantity of light falls within each band of the standard observer. The prorated quantities of light in each band are called XYZ, with X corresponding to the red region, and Y and Z corresponding to the green and blue regions (this process is illustrated in Figure 3). "Y" has a special additional meaning, having been defined in such a way that it corresponds to the measured luminance of the color, its gray level. This procedure is described in ASTM E308. Such a procedure, even though well explained in the ASTM document, is not trivial if colorimetry is just a tool and not your field of work. Luckily, most modern colorimeters and spectrophotometers compute these three coordinates directly from their measurements.

Let’s come back to our reference card and wall of a previous section. You are well aware that the color of a color card, even if this card subtends a larger than 10 degrees FOV, may look lighter than the same color applied to a large wall. This is due, in part, to the colored wall affecting the room lighting (the illuminant), which results in a shift of the perceived color, thus the importance of having a common mutually agreed specification and control method.
Surface finishes cover the entire range from ultra-matte (flat or lusterless) to shiny (brilliant or mirror-like). If we start from the same basic color, increasing the smoothness of the surface will make it look more and more like a mirror and you will be able to "see the light" at certain angles.

What this means in terms of perceived color is that you have a mix of the "true" color with the color of the illuminant, usually a variation on white, from yellowish to bluish.

If you want the color to be uniform from almost all points of views (both visual and personal), select a matte finish. The color will look deeper and more saturated. On the other hand, a brilliant finish may be in order to give a touch of luxury, as if covered with lacquer. In this case, you should expect to see a less saturated color than what the measured color coordinates indicate.

If the gloss effect is critical—let’s say that its importance is more than what can be controlled by simple variations of the raw materials used for the finish (different paint bases)—then you need to specify a gloss value and a tolerance (i.e. an error range, or gloss differential).

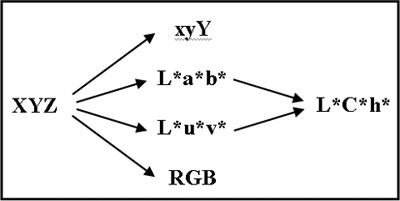
Figure 4: From XYZ, one can derive all the other standard CIE color notations, as well as RGB. The xyY representation is most often presented graphically. L*a*b*, L*u*v*, and L*C*h* are the color coordinates most used for specifications. RGB coordinates are dedicated to computer displays.

Starting with the XYZ data obtained by combining the characteristics of the colored sample with the ones of the illuminant, there is a collection of mathematical transformations that are available to obtain various output forms: xyY, L*a*b*, L*u*v*, and L*C*h* as shown in Figure 4. L*a*b* is pronounced L-star, a-star, b-star, and the asterisk is not a multiplication sign.
It was added to make a distinction with historically defined Lab, Luv and LCh notations.

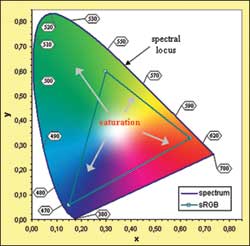
Figure 5: The CIE 1931 chromaticity diagram showing the xy coordinates of the xyY notation. The labels indicate the wavelength, in nm, and the locations of specific monochromatic colors. The primaries and the colors encompassed by the sRGB space, used to display images on most Windows-based computers, are also shown.

These color notations are all equivalent but present the information in complementary fashions. XYZ values are often seen in numerical form but seldom, if ever, presented graphically. The derived "xy"coordinates are, on the other hand, often presented in diagrams. The xy of the xyY notation are normalized values, between zero and one, of their XY counterparts. They are represented in the well-known "horseshoe" diagram of Figure 5, called a chromaticity diagram. The region within the horseshoe itself represents all the visible colors. The colors located on the horseshoe’s periphery, called the spectral locus, are pure, monochromatic, saturated colors. The more one goes toward its center, the less saturated a color becomes (i.e. it becomes whitish, grayish, or blackish). All illuminants of interest for practical uses are located in the center region. The "z" of xyz is seldom shown or given since, as a result of normalization, x+y+z=1. In addition, by normalizing, the actual luminance (Y) is lost; this is the reason for including Y as the third coordinate, instead of "z," when communicating color data (i.e. we use xyY instead of xyz).

The chromaticity diagram is very useful in presenting the relative positions of colors and can also be used to see what colors will result from mixing two others (for additive colors only, such as a computer screen, not for subtractive mixes like paint colors).

However, this color space, as with XYZ, is not perceptually uniform, and a given separation between two colors on the diagram corresponds to different perceived differences depending on their relative position.

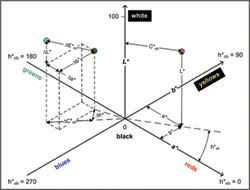
Figure 6: The L*a*b*/L*C*h* color space. On the right side we see how the a* and b* vectors are transformed in C* and h* (chroma and hue angle). On the left side, we see how a color difference is defined (more information on color difference will be presented in Part II).

L*a*b* and L*u*v* are attempts at making the XYZ (or xyY) space more perceptually uniform (see Figure 6). L* is the lightness, the intensity of the reflected light. Where Y represented the actual reflected energy, L* represents the perceived brightness, as the eye is not a linear sensor (exposing it to twice the energy will result in less than twice the perceived brightness). a* is the amount of red (+axis) or green (-axis) while b* is the amount of yellow (+axis) and blue (-axis); u* and v* have similar meanings. Red/green and blue/yellow are called “opponent” colors; you cannot perceive blue when there is yellow and vice-versa. Similarly, you cannot perceive red when there is green. Representing the colors in such a way is based on our understanding of how our brain processes colors.

Each notation, L*a*b* and L*u*v*, has its pros and cons, with different scaling factors for each variable, except L*, which is the same for both. But, in practice, L*a*b* is often preferred for printed color applications and L*u*v* for applications geared to electronic displays (especially in the U.K.).

L*C*h* is yet another transformation of either L*a*b* or L*u*v*, where the data is looked at from the perspective of cylindrical coordinates (see also Figure 6). C*, for chroma, or color saturation, a vector obtained by combining a* and b*, is the extent of the cylinder radius. h*, the hue angle, is the angle of the chroma vector. L*, the height of the chroma vector on the cylinder, is the same coordinate used in the L*a*b* and L*u*v* notations. Finally, starting with XYZ, you can also obtain RGB coordinates, as used in all computer displays. RGB stands for red, green, and blue, the colors of the primaries used on all video monitors (computers and TVs).

The conversion involves two steps, the first being a conversion from XYZ to linear RGB, and a second one, which scales the RGB values to match how we perceive brightness (called gamma correction), in a process similar to what is done between the "Y" of XYZ and the “L*” of L*a*b*. The first step, obtaining linear RGB values, requires the selection of the primaries, i.e. which colors correspond to pure R, G, and B (the apex of the sRGB triangle in Figure 5), as well as the selection of an illuminant. As no two RGB spaces have the same primaries, and often different illuminants and gamma corrections, the result is that identical RGB coordinates can basically describe any color, unless the space characteristics are known.

Why would you need to be concerned with RGB coordinates, you may ask? Well, if you want to accurately represent your project colors in printed documentation, in CAD renderings, or use them on the Web, you need to know their RGB equivalent.

In many instances, it is required to obtain the coordinates of a sample for a different illuminant than the one used for the original data. For example, your requirement calls for a color specified in L*a*b* D65 coordinates and your measuring instrument gives you L*a*b* D50 data. Since color coordinates are closely associated to the illuminant used to measure them, the most accurate method is to take the spectral reflection ratios obtained with D50, and recalculate the coordinates using the spectral emission curve of D65 with the method described in ASTM E308 (same standard observer, different illuminant).

The problem is that often the spectral data of the sample is not available (a colorimeter does not give you spectral data, a spectrophotometer does), and the only information you have is three color coordinates. The solution is to use an approximate method, called a Chromatic Adaptation Transform, which applies a matrix transform directly to the coordinates. Such a matrix can be derived for each pair of illuminants, such as when going from D65 to D50, or from C to D50. Some mathematical knowledge is required but some tools are designed to handle this task easily.

This concludes the first "theoretical" part of the article. In Part II you will see examples of how these multiple notations are dealt with in real life.

Editor's Note:

This is the first of a two-part series. Part II will appear in the February issue.

After many years of research and development and project management work in the academic and industrial sectors, Danny Pascale now does technology assessment and helps companies bring new products into the market in the computer and consumer electronics industries. He recently formed a new company, The BabelColor, dedicated to the development of colorimetric software tools.